Denníček

13.9. utorok:

Poskladali sme väčšinu modelov, ostal nám len transport zvierat, plameniak a dojací stroj. Chýbal nám jeden sáčok č.7, ale chýbajúce súčiastky sme nahradili našimi vlastnými.

20.9. utorok:

Dostali sme na krúžok stôl, takže sme ponalepovali Dual Locky a dostavali všetky modely. Pozreli sme si video so zadaním úloh a rozmýšľali sme nad zadaniami.

22.9. štvrtok:

Vytvorili sme si prvú verziu webstránky krúžku. Zapísali sme si prehľadné bodovanie úloh a diskutovali sme nad možným poradím plnenia úloh, ktoré sme si zapísali a nakreslili v obrázku, ktorý ešte prekreslíme, aby vyzeral pekne.

Skúšali sme ďalekonosné doručovanie koláčov a zostrojili bránku, ktorá ich efektívne zachytí a odrazí do výskumnej a tréningovej oblasti.

Diskutovali sme o problémoch zvierat - o prehriatom Potkanovi a o morskom prasiatku, ktoré zahynulo, lebo sa s ním hralo malé dievčatko bez dozoru rodičov.

Dohodli sme sa, že na každom krúžku si povieme príbehy o zvieratkách, ktoré sme počuli alebo čítali alebo zažili.

27.9. utorok:

snazime sa spravit prvych par krokov na zaciatok maximalnej jazdy a zaciname diskutovat o konstrukcii a vzhlade robota
niektorí sa snazia zacat vyskumny projekt. Tiger vyrobil prvú verziu doplnku na prevážanie žraloka, ale zdá sa, že má priveľa stupňov voľnosti. Patrik stavia robota. Krotiteľ hadov poskladal z druhej stavebnice základný model a programoval ho priamo na kocke EV3.

29.9. štvrtok:

Prvá verzia základného robota, ktorý jazdí, je hotová. Je ešte trochu nestabilný, ale keď bude jazdiť veľkými kolesami vpred a zrýchľovať a spomaľovať pomaly, tak by asi bol použiteľný. Má dva motory pre riadenie primontovaných doplnkov. Ešte potrebuje senzory! Krotiteľ hadov napísal svoje prvé programy v programovacom jazyku EV3 na počítači: robot sa pohyboval vpred až kým neprišiel k domčeku, potom sa otočil a zaklopal na dvere. Tiger poskladal novú verziu ruky na posun žraloka, ktorá by mohla fungovať bez motora, ale ešte treba vymyslieť ako ju namontovať na robota.

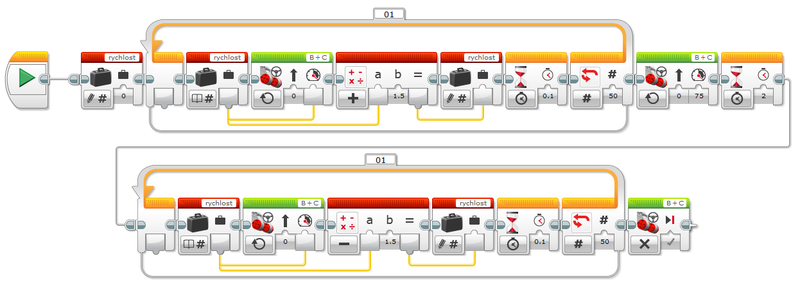
Tiger sa naučil programovať vlastné bloky pre EV3 - vytvorili sme blok, ktorý postupne zrýchľuje asi 5 sekúnd z 0 na 75, potom ide dve sekundy rýchlosťou 75 a potom zasa spomaľuje 5 sekúnd zo 75 na 0. Používa pritom premennú rýchlosť a matematický blok (sčítanie a odčítanie), pričom 50-krát za sebou vždy pridá alebo odoberie hodnotu 1.5:

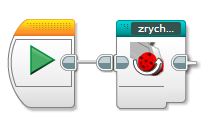
použitie vlastného bloku:

Download: zrychlenie.zip

Nabudúce by sme sa mohli naučiť ako tomuto bloku nastaviť vstupné hodnoty - tak, aby zrýchlil na požadovanú rýchlosť (nie vždy na 75) a aby prešiel požadovanú vzdialenosť (a nie vždy 12 sekúnd).

Žralok zostrojil prvú verziu dávkovača krmiva:

Nezabudnite na nové príbehy o zvieratkách!

4.10. utorok:

Ružový panter rozobral hlavného robota :-D.

naštastie :-) sme ho zavčasu zastavili, ale bol dosť šikovný, aby ho znovu poskladal.
Nebránime sa dobrým nápadom a novým myšlienkam, robot zatiaľ nie je dokonalý a určite sa dá zlepšovať, ale treba dať pozor, aby sme sa na tom dohodli ako celý tím. Nezávislá iniciatíva, ktorá pomení výledok niekoľkých hodín práce ostatných, ktorí sa k tomu nemôžu vyjadriť - tomu sa určite chceme vyvarovať!

Dnes sa nám podarilo:

• zistili sme, že dávkovač krmiva, ktorý Žralok minule poskladal potrebuje zarážku, aby posuvník nevybehol do polohy, kde ho už ozubené koliesko nezachytí - na druhý pokus sme zarážku umiestnili dobre a dávkovač už dávkoval spoľahlivo.
• ale - keďže asi bude namontovaný na robotovi vysoko, vysypané krmivo odskakuje ďaleko z kruhovej oblasti zvieraťa, preto mrož poskladal dávkovaciu rúru, cez ktorú sa krmivo vysype až na zem a neodskakuje
• dotiahli sme mechaniku konštrukcie na transport žraloka - bolo treba vymeniť strany (robot musí ísť kolesami napred cez slepecký plot) a vďaka tomu je rameno uchytené na takom mieste, že stačí otočiť len jedným kolesom a robot sa z neho vyvlečie, zdá sa, že to funguje spoľahlivo. ostáva vytvoriť program - ale to sa musíme najskôr naučiť pohybovať opatrne
• žralok rozrobil prvú verziu nadstavca na vykladanie zvierat na mechanizmus výmeny zvierat...
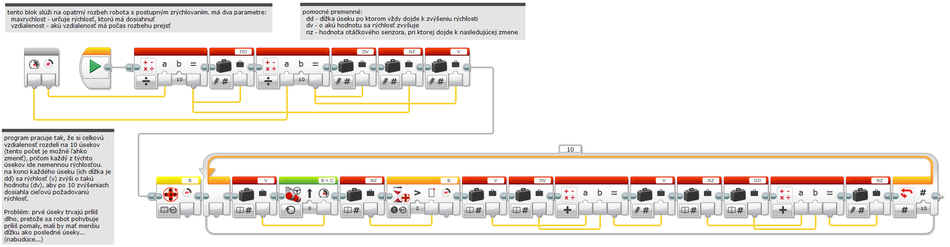
• naprogramovali sme náš prvý blok so vstupnými parametrami: blok na opatrné rozbiehanie sa, ktorý postupne zvyšuje rýchlosť. Má dva parametre: 1) celkovú vzdialenosť na ktorej má zrýchliť z nulovej až do výslednej rýchlosti a 2) výslednú rýchlosť na ktorú má zrýchliť
• na tento blok by mali nadväzovať blok na pohyb stálou rýchlosťou a opačný blok - ktorý bude postupne spomaľovať.
• celkom na konci sme zistili, že blok má jeden problém - prečítaj si na obrázku dole - nabudúce ho skúsime vyriešiť.

Download: opatrnost.zip

• diskutovali sme o tom, že pri zbieraní úrody na poliach kombajnami sa stáva, že kombajn pokosí aj mladú srnku, zajaca, alebo iné zvieratá - rozmýšľali sme nad quadkoptérou, ktorá by letela pred kombajnom a kontrolovala pole pohľadom priamo zhora, prípadne nad ramenom, ktoré by sa počas kosenia vysunulo a plnilo by rovnakú funkciu. Zamýšľali sme sa nad tým, či nejake iné senzory by dokázali zistiť, či sa v poli nachádzajú nejaké zvieratá...

6.10. stvrtok:

• Palo tu s nami bol len chvílu )-: //Paľo: lebo prišiel Matej, ktorý sa vám venoval, teda dúfam :-)
• Prijali sme 2 nových žiakov // no len či prídu obaja znovu :-)
• do 999/1000 sme dorobili zrýchľovanie (-: // tak na to sa ešte pozrieme

11.10. utorok:
Dnes sa pracovalo, ale neviem, neviem, koľko užitočného sa urobilo... ale snáď aspoň niečo. V každom prípade treba výmyšľať a skúšať nové nápady a aj keď nevýjdu, tak sa na tom vždy niečo naučíme.

• Krotiteľ poskladal krabičku pre zachytenie krmiva, ktoré sa vysype z dávkovača krmiva a bude ho treba k dávkovaču doviezť asi v prvej jazde.
• Žralok sa pokúsil zostrojiť systém na vykladanie zvierat na otočnú platformu, ktorý by fungoval bez motora na princípe zošmyknutia sa prevážaného zvieraťa. Problémik je v tom :-), že zvieratko takto väčšinou zakopne a prevalí sa ďalej až spadne - pozri obrázok - obzvlášť netopier sa takto rád správa, keďže jeho stabilita kvôli hojdajúcemu sa netopierovi na konári nie je veľká...
• Tiger s Panterom sa pustili do prestavovania automatickej pušky na odstreľovací mechanizmus na koláče, aby sme ich zo základne všetky mohli rýchlo odstreliť do výskumnej a tréningovej oblasti (štvorec za zelenou rampou). Vyskúšali, že motor by aj mohol mať silu na odstrelenie koláčov, ale plochu treba dať dolu na stôl, prípadne ju dať celkom preč, aby sa koláče mohli kĺzať priamo po povrchu ihriska a nechať tam iba odstreľovací prevod pripojiteľný na motor - tam bude treba hlavne vymyslieť, ako pripojiť tento mechanizmus na niektorý z motorov robota... napríklad namiesto jedného z jeho kolies?
• Mrož veľmi usilovne budoval dávkovač koláčov, ktorý na jednu stranu vyhadzuje oddeľovacie prepážky a na druhú stranu koláče. Je však otázka, či tento mechanizmus bude treba. Ak sa budú koláče kĺzať priamo po povrchu ihriska, tak ich pred robota obsluhujúci technici počas hry môžu položiť priamo rukou aj počas práce robota - len sa nesmú dotknúť ničoho, čo je s robotom pevne spojené!
• Maťo - ktoré si zviera? :-) sa učil programovať robota, ktorý jazdí po čiare a vcelku sa mu to podarilo!
• A krotiteľ pracoval na bloku na postupné zrýchľovanie. Vymyslel novú verziu, kde robot každú desatinku sekundy zvýši rýchlosť o 1 - takže by sa už nemalo stávať, že na začiatku mu trvá dlho, kým prejde prvý úsek, zatiaľ čo posledný úsek prefičí za veľmi krátky čas. Keď robot dosiahol maximálnu rýchlosť alebo došiel do požadovanej vzdialenosti, tak cyklus skončil. A tu je práve ten problém - v tom slovíčku ALEBO. My by sme potrebovali, aby vždy došiel do požadovanej vzdialenosti a okrem toho aby na konci mal požadovanú rýchlosť, pričom sa k nej dopracuje postupne... Takže musíme ísť na to ešte raz. Rozmýšľali sme nad problémom spoločne a prišli sme na toto:

Z matematiky vieme (Žralok vysypal vzorec z rukáva), že súčet prvých N po sebe idúcich čísel je rovný 1 + 2 + 3 + ... + n = n * (n + 1) / 2. Napríklad:

1 + 2 + 3 = 6 = 3 * 4 / 2
1 + 2 + 3 + 4 = 10 = 4 * 5 / 2
1 + 2 + 3 + 4 + 5 = 15 = 5 * 6 / 2
...

Žralok hneď aj vysvetlil prečo to tak je - lebo môžeme dať vždy do dvojíc postupne čísla, ktoré odoberáme zľava a čísla, ktoré odoberáme zprava a dostávame vždy súčet n + 1: Napr. pre

1 + 2 + 3 + 4 + 5 + 6, čiže n = 6, vytvárame dvojice:

1 + 6 = 7 = (6 + 1) = (n + 1)
2 + 5 = 7 = (6 + 1) = (n + 1)
3 + 4 = 7 = (6 + 1) = (n + 1)

a keďže naraz odoberáme z oboch strán, tak takýchto dvojíc vytvoríme polovičný počet oproti pôvodnému počtu čísel, čiže n / 2. Celkovo teda môžeme vypočítať súčet 1 + 2 + 3 + 4 + 5 + 6 tak, že posčitujeme namiesto pôvodných n čísel, tých n/2 dvojíc. Každá dvojica má súčet n + 1 a je ich n / 2, takže súčet je (n + 1) * n / 2. (keby to niekoho veľmi zaujímalo - sedí to aj pre nepárne n, lebo ten stredný, čo ostane je práve = (n + 1) / 2 a dvojíc je pre nepárny prípad len n / 2 - 1/2.)

Ako tento vzorec súvisí s našim problémom postupného zrýchľovania?

chceli by sme, aby sa robot pohyboval postupne zvyšujúcou sa rýchlosťou a na konci dosiahol rýchlosť v. Prvý úsek prejde desatinovou rýchlosťou v/10, druhý úsek dvojdesatinovou 2 * v/10 atď až posledný úsek prejde desaťdesatinovou rýchlosťou 10 * v/10, čiže výslednou rýchlosťou v. Lenže my by sme chceli, aby týmito rýchlosťami išiel postupne vždy rovnako dlho = rovnaký čas a nie rovnakú dráhu, ako sme naprogramovali minule. Z fyziky niektorí už vieme, ako súvisia dráha, čas a rýchlosť:

s = v * t

s - dráha
v - rýchlosť
t - čas

celkový súčet jednotlivých dráh pre všetkých 10 úsekov by mal dávať celú dráhu, ktorú robot má prejsť:

s = s1 + s1 + ... + s10

kde

s1 - je dráha akú prejde robot v prvom úseku rýchlosťou v / 10
s2 - je dráha akú prejde robot v druhom úseku rýchlosťou 2 * v / 10
...
s10 - je dráha akú prejde robot v poslednom úseku rýchlosťou 10 * v / 10

každý úsek má prejsť za rovnaký čas, označme ho t₁.

Takže pre jednotlivé úseky platí:

s1 = v / 10 * t1
s2 = 2 * v / 10 * t1
s3 = 3 * v / 10 * t1
...
s10 = 10 * v / 10 * t1

keď ich posčitujeme, dostaneme

s = v / 10 * t1 + 2 * v / 10 * t1 + 3 * v / 10 * t1 + ... + 10 * v / 10 * t1

s = v / 10 * t1 * (1 + 2 + 3 + ... + 10) 

s = v / 10 * t1 * (10 * 11 / 2) = v * t1 * 11 / 2

čiže

t1 = s / v * 2 / 11

a potom

s1 = v / 10 * t1 = s * 1 / 55
s2 = 2 * v / 10 * t1 = s * 2 / 55
s3 = 3 * v / 10 * t1 = s * 3 / 55
... 
s10 = 10 * v / 10 * t = s * 10 / 55

a teraz už iba zostáva ten pôvodný program upraviť! :-) teda tak, aby dĺžka prejdených úsekov nebola rovnaká ako v pôvodnom programe, ale sa postupne menila tak, ako je to vypočítané v týchto vzorcoch.

Dnešné obrázky: